卡尔曼滤波
为什么要使用跟踪预测算法
在深入研究卡尔曼滤波器之前,我们首先来了解跟踪和预测算法的必要性。
为了说明这一点,让我们以一个雷达跟踪目标为例。
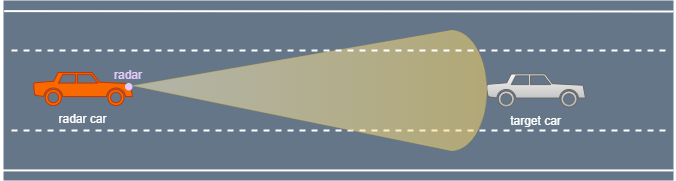
假设雷达每隔 1 s 对目标进行采样,进而估计目标当前的位置和速度。雷达同时还能根据牛顿运动方程估计(或预测)目标下一个测量周期的位置和速度。
| $x = x_0 + v_0 \cdot \Delta t + {1 \over 2} a \cdot \Delta t^2$ $v = v_0 + a \cdot \Delta t$ |
|---|
| $x$ 是目标位置 $x_0$ 是初始目标位置 $v$ 是目标速度 $v_0$ 是初始目标速度 $a$ 是目标加速度 $\Delta t$ 是采样周期 |
$[x,v,a]$ 称为系统状态。当前状态作为预测算法的输入,预测算法的输出则是目标下一时刻的状态。
上面的牛顿运动方程组称为动态模型或状态空间模型。状态空间模型描述了预测算法的输入和输出之间的关系。
显然,如果已知目标的当前状态和状态空间模型,那么就可以很简单地预测目标未来的状态。
实际场景中,雷达的测量并不完全准确,它所包含的随机噪声或不确定性会影响对目标状态的测量精准度。误差大小取决于多方面因素,例如雷达校准、回波信噪比等。雷达测量的随机噪声或不确定性称为测量噪声。
另外,由于存在风扰、驾驶员干预等因素,目标的运动并不总能依照运动方程。运动目标的预测和实际目标的运动轨迹之间的差异称为过程噪声。
由于测量噪声和过程噪声的存在,估计目标的位置有可能和目标的真实位置相差很大。为了提升雷达跟踪的精准度,就需要一套能对抗测量和状态空间模型的不确定性的预测算法。卡尔曼滤波就是最常用的跟踪和预测算法。
卡尔曼滤波方程
卡尔曼滤波有五个关键方程。
两个预测方程:
- 状态预测方程-基于当前的估计来预测或估计未来的状态。
- 协方差预测方程-未来状态预测的不确定性度量。
两个更新方程:
- 状态更新方程-基于上一时刻的预测值和当前的测量值来估计当前的状态。
- 协方差更新方程-当前状态估计的不确定性度量。
一个权重系数方程:
卡尔曼增益方程-两个更新方程中会用到。卡尔曼增益是测量值和预测值的“权重系数”,它表明了应该相信多少过去的预测值,又应该相信多少当前的测量值。
| 方程 | 方程名 |
|---|---|
| $K_n = {p_{n,n-1} \over p_{n,n-1} + r_n}$ | 卡尔曼增益方程或权重方程 |
| $\hat x_{n,n} = \hat x_{n,n-1} + K_n \left(z_n - \hat x_{n,n-1}\right)$ | 状态更新方程或滤波方程 |
| $p_{n,n} = \left( 1 - K_n \right)p_{n,n-1}$ | 协方差更新方程或修正方程 |
| $\hat x_{n+1,n} = \hat x_{n,n}$ (恒定状态空间模型) $\hat x_{n+1,n} = \hat x_{n,n} + \triangle t \cdot \hat x^v_{n,n}$ $\hat x^v_{n+1,n} = \hat x^v_{n,n}$ (速度恒定状态空间模型) |
状态预测方程或状态外插方程或状态空间模型 |
| $p_{n+1,n} = p_{n,n}$ (恒定状态空间模型) $p^x_{n+1,n} = p^x_{n,n} + \triangle t^2 \cdot p^v_{n,n}$ $p^v_{n+1,n} = p^v_{n,n}$ (速度恒定状态空间模型) |
协方差预测方程或协方差外插方程 |
说明
- 状态预测方程和协方差预测方程都依赖于系统动态模型。
- 为了理解卡尔曼滤波的基本原理和概念,表中所描述的卡尔曼滤波方程是针对特定问题的特定形式。其一般形式通常会以矩阵形式给出。
接下来,我们推导状态更新方程。
状态更新方程推导
我们能否将雷达的测量值和预测值融合在一起,从而估计出目标当前状态。能快速想到的就是将测量值和状态预测值进行加权求和:
| $\hat x_{n,n} = w_1 \cdot z_n + w_2 \cdot \hat x_{n,n-1}$ $w_1 + w_2 = 1$ |
|---|
| $\hat x_{n,n}$ 是 $n$ 时刻的状态估计值 $\hat x_{n,n-1}$ 是在 $n-1$ 时刻对 $n$ 时刻的状态预测值 $w_1$ 是测量值的权重 $w_2$ 是预测值的权重 |
$\hat x_{n,n}$ 可以写作:
| $\hat x_{n,n} = w_1 \cdot z_n + (1-w_1) \cdot \hat x_{n,n-1}$ $\space \space \space \space \space \space \space \space = w_1 \cdot z_n + \hat x_{n,n-1} - w_1 \cdot \hat x_{n,n-1}$ $\space \space \space \space \space \space \space \space = \hat x_{n,n-1} + w_1 \cdot (z_n - \hat x_{n,n-1})$ |
|---|
| 我们将 $w_1$ 替换为 $K_n$ 就可以得到卡尔曼滤波的状态更新方程: $\hat x_{n,n} = \hat x_{n,n-1} +K_n \cdot (z_n - \hat x_{n,n-1})$ $K_n$ 具有下标 $n$ 意味着卡尔曼增益随着每次迭代都会改变。 |
上述状态更新方程中,还有两个待解决的问题:
- 如何求解 $\hat x_{n,n-1}$
- 如何获得 $K_n$
接下来,我们就先来推导卡尔曼增益方程 $K_n$ 。
卡尔曼增益方程推导
卡尔曼滤波将测量值、当前状态估计和下一个状态预测均视为具有正态分布的随机变量,这些随机变量由均值和方差进行描述。
因此,我们可以将当前状态估计值的不确定性和测量值的不确定性分别用方差 $p_{n,n}$ 和 $r_n$ 来表示。
根据方程:
\[\hat x_{n,n} = w_1 \cdot z_n + (1-w_1) \cdot \hat x_{n,n-1}\]可以将估计值的方差与测量值的方差之间的关系记为:
$p_{n,n} = w_{1}^{2} \cdot r_n + (1- w_1)^2 \cdot p_{n,n-1}$
$p_{n,n}$ 是最优估计值 $\hat x_{n,n}$ 的方差
$p_{n,n-1}$ 是状态预测值 $\hat x_{n,n-1}$ 的方差
$r_n$ 是测量值 $z_n$ 的方差
卡尔曼滤波器是一种最优滤波器,最优性体现在它能够把状态预测值和测量值融合在一起,使得计算的当前状态估计值的不确定性最小。
为了找到能最小化 $p_{n,n}$ 的 $w_1$ ,我们把 $p_{n,n}$ 对 $w_1$ 求导,并令导数为零。
\[{d_{p_{n,n}} \over d_{w_1}} = 2w_1 \cdot r_n - 2(1-w_1) \cdot P_{n,n-1} = 0\]计算可以得到 $w_1$:
\[w_1 = {p_{n,n-1} \over p_{n,n-1} + r_n}\]把上述结果代入当前状态估计方程: $\hat x_{n,n} = w_1 \cdot z_n + (1-w_1) \cdot \hat x_{n,n-1}$ ,可以得到方程:
\[\hat x_{n,n} = \hat x_{n,n-1} + {p_{n,n-1} \over p_{n,n-1} + r_n} \cdot (z_n - \hat x_{n,n-1})\]由此可得到卡尔曼增益方程:
| $K_n = {p_{n,n-1} \over p_{n,n-1} + r_n}$ |
|---|
| $p_{n,n-1}$ 是状态预测的方差 $r_n$ 是测量值的方差 |
测量值的方差 $r_n$ 可以从测量设备厂商获取,根据数据计算,或通过校准程序推导。
对于雷达来说,测量值的不确定性受很多因素影响,例如信噪比、波束宽度、照射时长等。因此雷达需要自行计算每次测量的不确性。
把状态更新方程等效变换一下,可以得到:
\[\hat x_{n,n} = \hat x_{n,n-1} + K_n \cdot (z_n - \hat x_{n,n-1}) = K_n \cdot z_n + (1-K_n) \cdot \hat x_{n,n-1}\]可见,卡尔曼增益 $K_n$ 是测量值的权重, $1-K_n$ 则是当前状态预测值的权重。
卡尔曼增益在测量不确定性很高而预测不确定性很低的时候接近 $0$ ,故当前状态预测值的权重很高,测量值的权重很低。
相反地,卡尔曼增益在测量不确定性很低而预测不确定性很高的时候接近 $1$ ,故当前状态预测值的权重很低,测量值的权重很高。
如果测量值和预测值的不确定性相同,则卡尔曼增益等于 $0.5$ 。
在估计新的状态的时候,卡尔曼增益定义了测量值和状态预测值的权重,表明有多少新的测量值应该进入最后的估计值。
解决了卡尔曼增益方程,我们又引入了一个状态预测的方差 $p_{n,n-1}$ 需要解决。
到目前为止,我们仍然有两个问题待解决:
- 如何求解 $\hat x_{n,n-1}$
- 如何获得 $p_{n,n-1}$
这两个问题都跟预测有关,待我们完成协方差更新方程推导之后再来解决这两个问题。
协方差更新方程推导
前文的 $w_1$ 就是卡尔曼增益 $K_n$,因此可以根据估计值的方差于测量值得方差关系方程 $p_{n,n} = w_{1}^{2} \cdot r_n + (1-w_1)^2 \cdot p_{n,n-1}$ 进行如下推导:
| 推导 | 注解 |
|---|---|
| $p_{n,n} = w_{1}^{2} \cdot r_n + (1-w_1)^2 \cdot p_{n,n-1}$ | 将 $K_n$ 替换掉 $w_1$ |
| $p_{n,n} = K_{n}^{2}r_n + (1-K_n)^2P_{n,n-1}$ | 将卡尔曼增益 $K_n$ 代入 |
| $p_{n,n} = ({p_{n,n-1} \over p_{n,n-1} + r_n})^2r_n + ({r_n \over p_{n,n-1} + r_n})^2P_{n,n-1}$ | 把展开后的 $K_n$ 和 $(1 - K_n)$ 代入 |
| $p_{n,n} = { p_{n,n-1}^{2}r_n \over (p_{n,n-1} + r_n)^2} + {r_{n}^{2} p_{n,n-1} \over (p_{n,n-1} + r_n)^2}$ | 展开平方 |
| $p_{n,n} = {p_{n,n-1}r_n \over p_{n,n-1}+r_n}({p_{n,n-1} \over p_{n,n-1} + r_n} + {r_n \over p_{n,n-1} + r_n})$ | 提出共有项 |
| $p_{n,n} = (1 - K_n)p_{n,n-1}(K_n + (1 - K_n))$ | 再代入 $K_n$ 和 $(1 - K_n)$ |
| $p_{n,n} = (1 - K_n)p_{n,n-1}$ | $K_n$ 抵消 |
由此可以得到协方差更新方程:
$p_{n,n} = (1 - K_n) \cdot p_{n,n-1}$
卡尔曼增益是一个 $0$ 到 $1$ 之间的数,从方程可以看出,因为有 $(1 - K_n) \le 1$ ,状态估计的不确定性是始终在随着滤波器迭代而下降的。当测量不确定性很高的时候,卡尔曼增益很低,因此状态估计不确定性收敛的速度会变慢。相反,当测量不确性很低的时候,卡尔曼增益则很高,故状态估计不确定性会快速收敛到 $0$ 。
所以实际场景中需要我们确定到底要测量和迭代多少次来获得一个足够确定的估计值。
最后,我们来解决剩下的两个问题:
- 如何求解 $\hat x_{n,n-1}$
- 如何获得 $p_{n,n-1}$
只有解决了这两个问题,整个卡尔曼滤波方程才能完成闭环。因为这两个问题都属于系统预测的部分,它们跟系统的状态空间模型有关,因此不同的状态空间模型会有不同的 $\hat x_{n,n-1}$ 和 $p_{n,n-1}$ 。
状态预测方程推导
因为不同系统的状态空间模型是有区别的,同样的,其状态预测方程也是有所区别的。下面考虑雷达车与目标车运动的几种情况:
-
雷达车静止,目标车静止
这种情况可以认为系统状态空间模型是恒定的,也就是说当前时刻对下一时刻 $x$ 的预测值等于当前时刻对 $x$ 的估计值,其距离的状态预测方程为:
\[\hat x_{n+1,n} = \hat x_{n,n}\] -
雷达车静止,目标车匀速直线运动
根据牛顿运动方程,我们可以得到距离,速度的状态预测方程:
\[\hat x_{n+1,n} = \hat x_n + \hat v_n \cdot \Delta t\] \[\hat v_{n+1} = \hat v_n\] -
雷达车静止,目标车加速直线运动
根据牛顿运动方程,我们可以得到距离,速度,加速度的状态预测方程:
\[\hat x_{n+1,n} = \hat x_{n,n} + \hat v_{n,n} \cdot \Delta t + 0.5 \cdot \hat a_{n,n} \cdot \Delta t^2\] \[\hat v_{n+1,n} = \hat v_{n,n} + \hat a_{n,n} \cdot \Delta t\] \[\hat a_{n+1,n} = \hat a_{n,n}\]
雷达车运动和目标车静止,雷达车和目标车同时运动等其它情况,本次分享暂时不做考虑
协方差预测方程推导
跟状态预测方程一样,协方差预测方程也是跟系统有关。接下来,我们考虑上面雷达车与目标车的三种情况下,协方差预测方程是怎么样的。
-
雷达车静止,目标车静止 \(p^x_{n+1,n} = p^x_{n,n}\)
-
雷达车静止,目标车匀速直线运动
对任何服从方差为 $\delta^2$ 的正态分布的随机变量 $x$ , $kx$ 服从方差为 $k^2\delta^2$ 的正态分布,因此位置估计的方差更新时速度估计的方差所乘的项为时间间隔的平方。
\(p^x_{n+1,n} = p^x_{n,n} + \Delta t^2 \cdot p^v_{n,n}\) \(p^v_{n+1,n} = p^v_{n,n}\)
-
雷达车静止,目标车加速直线运动 \(p^x_{n+1,n} = p^x_{n,n} + p^v_{n,n} \cdot \Delta t^2 + 0.25 \cdot p^a_{n,n} \cdot \Delta t^4\) \(p^v_{n+1,n} = p^v_{n,n} + p^a_{n,n} \cdot \Delta t^2\) \(p^a_{n+1,n} = p^a_{n,n}\)
$p^x$ 是位置估计的方差
$p^v$ 是速度估计的方差
$p^a$ 是加速度估计的方差
到此,卡尔曼滤波方程,全部推导完成。
卡尔曼滤波的底层结构描述
因为卡尔曼滤波方程存在 $n-1$ 时刻对 $n$ 时刻状态的预测,因此需要一个初始化猜测,也即滤波器需要一个初始化输入。
初始化输入过程只进行一次,负责提供两个参数:初始化状态 $\hat x_{0,0}$ 和初始状态方差 $p_{0,0}$ 。
初始化参数可以由其他的系统或基于经验和理论知识所得出的合理猜测来获得。即使初始化参数不太准确,卡尔曼滤波器也能收敛到接近真值。
卡尔曼滤波可以由“测量,更新,预测”三个核心步骤来描述。下图给出了卡尔曼滤波的详细框图描述:
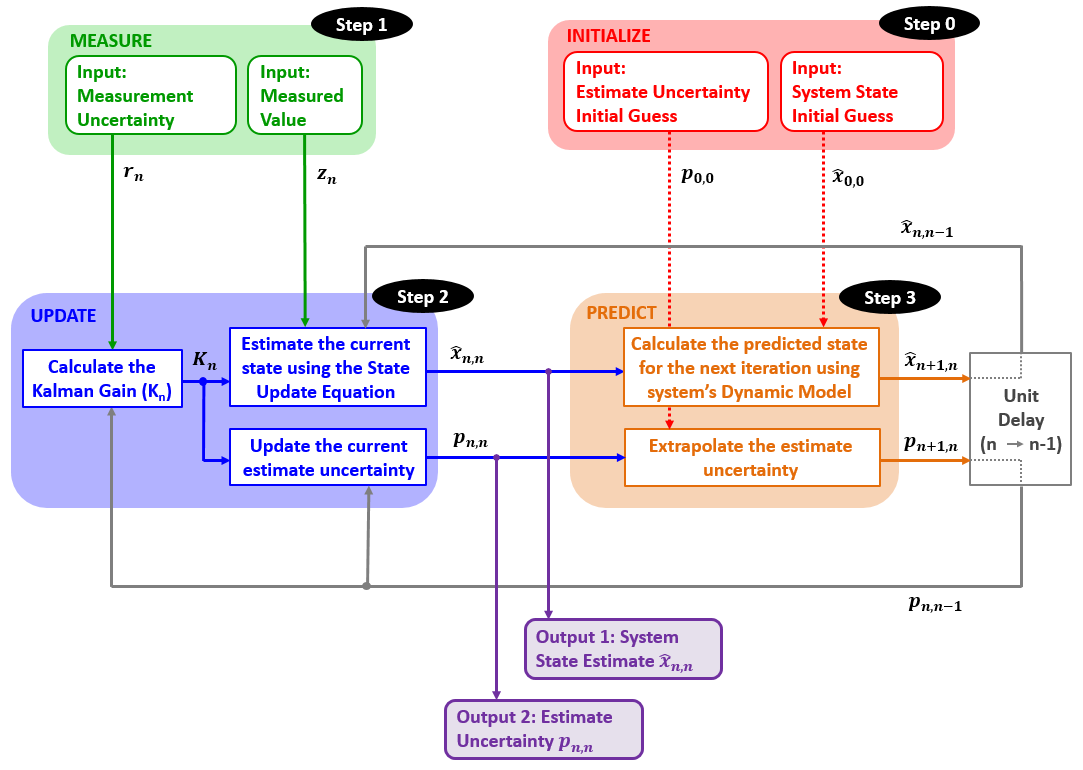
示例-雷达跟踪直线匀速运动的目标车
根据卡尔曼滤波的状态更新方程和牛顿运动方程可以得到该系统距离,速度的状态更新方程为:
\[\hat x_{n,n} = \hat x_{n,n-1} + K^x_n \cdot (z_n - \hat x_{n,n-1})\] \[\hat v_{n,n} = \hat v_{n,n-1} + K^v_{n} \cdot ({z_n - \hat x_{n,n-1} \over \Delta t})\]根据牛顿运动方程可以得到该系统距离,速度的状态预测方程分别为:
\[\hat x_{n+1,n} = \hat x_{n,n} + \hat v_{n,n} \cdot \Delta t\] \[\hat v_{n+1,n} = \hat v_{n,n}\]根据牛顿运动方程可以得到该系统距离,速度的协方差预测方程为:
\[p^x_{n+1,n} = p^x_{n,n} + p^v_{n,n} \cdot \Delta t^2\] \[p^v_{n+1,n} = p^v_{n,n}\]假设雷达距离,速度的测量误差分别为 $r^x_n=0.01$ 和 $r^v_n = 0.04$,周期 $1 \space s$
则该系统距离,速度的卡尔曼增益方程分别为:
\[K^x_n = {p^x_{n,n-1} \over p^x_{n,n-1} + 0.01}\] \[K^v_{n} = {p^v_{n,n-1} \over p^v_{n,n-1} + 0.04}\]该系统距离,速度的协方差更新方程分别为:
\[p^x_{n,n} = (1 - K^x_n) \cdot p^x_{n,n-1} = {0.01 \cdot p^x_{n,n-1} \over p^x_{n,n-1} + 0.01}\] \[p^v_{n,n} = (1 - K^v_n) \cdot p^v_{n,n-1} = {0.04 \cdot p^v_{n,n-1} \over p^v_{n,n-1} + 0.04}\]下面是 10 次迭代各状态的值:
| 第 $n$ 次迭代 | $z_n$ | 当前状态估计( $\hat x_{n,n}$, $\hat v_{n,n}$, $K_n$, $p_{n,n}$ ) | 未来状态预测( $\hat x_{n+1,n}$, $\hat v_{n+1,n}$, $p_{n+1, n}$ ) |
|---|---|---|---|
| $0$ | - | $\hat x_{0,0} = 10 \space m$ $\hat v_{0,0} = 20 \space m/s$ $p^x_{0,0} = 0.01$ $p^v_{0,0} = 0.09$ |
$\hat x_{1,0} = 30 \space m$ $\hat v_{1,0} = 20 \space m/s$ $p^x_{1,0} = 0.1$ $p^v_{1,0} = 0.09$ |
| $1$ | $28m$ | $K^x_1 = 0.909091$ $K^v_1 = 0.692308$ $\hat x_{1,1} = 28.18 \space m$ $\hat v_{1,1} = 18.62 \space m/s$ $p^x_{1,1} = 0.009091$ $p^v_{1,1}=0.027692$ |
$\hat x_{2,1} = 46.8 \space m$ $\hat v_{2,1} = 18.62 \space m/s$ $p^x_{2,1} = 0.036783$ $p^v_{2,1} = 0.027692$ |
| $2$ | $45m$ | $K^x_2 = 0.786248$ $K^v_2 = 0.409091$ $\hat x_{2,2} = 45.38 \space m$ $\hat v_{2,2} = 17.88 \space m/s$ $p^x_{2,2} = 0.007862$ $p^v_{2,2}=0.016364$ |
$\hat x_{3,2} = 63.26 \space m$ $\hat v_{3,2} = 17.88 \space m/s$ $p^x_{3,2} = 0.024226$ $p^v_{3,2} = 0.016364$ |
| $3$ | $67m$ | $K^x_3 = 0.707825$ $K^v_3 = 0.290323$ $\hat x_{3,3} = 65.91 \space m$ $\hat v_{3,3} = 18.96 \space m/s$ $p^x_{3,3} = 0.007078$ $p^v_{3,3}=0.011613$ |
$\hat x_{4,3} = 84.87 \space m$ $\hat v_{4,3} = 18.96 \space m/s$ $p^x_{4,3} = 0.018691$ $p^v_{4,3} = 0.011613$ |
| $4$ | $85m$ | $K^x_4 = 0.651461$ $K^v_4 = 0.225$ $\hat x_{4,4} = 84.96 \space m$ $\hat v_{4,4} = 19 \space m/s$ $p^x_{4,4} = 0.006515$ $p^v_{4,4}=0.009$ |
$\hat x_{5,4} = 103.95 \space m$ $\hat v_{5,4} = 19 \space m/s$ $p^x_{5,4} = 0.015515$ $p^v_{5,4} = 0.009$ |
| $5$ | $108m$ | $K^x_5 = 0.608068$ $K^v_5 = 0.183673$ $\hat x_{5,5} = 106.41 \space m$ $\hat v_{5,5} = 19.74 \space m/s$ $p^x_{5,5} = 0.006081$ $p^v_{5,5}=0.007347$ |
$\hat x_{6,5} = 126.15 \space m$ $\hat v_{6,5} = 19.74 \space m/s$ $p^x_{6,5} = 0.013428$ $p^v_{6,5} = 0.007347$ |
| $6$ | $130m$ | $K^x_6 = 0.573153$ $K^v_6 = 0.155172$ $\hat x_{6,6} = 128.36 \space m$ $\hat v_{6,6} = 20.33 \space m/s$ $p^x_{6,6} = 0.005732$ $p^v_{6,6}=0.006207$ |
$\hat x_{7,6} = 148.69 \space m$ $\hat v_{7,6} = 20.33 \space m/s$ $p^x_{7,6} = 0.011938$ $p^v_{7,6} = 0.006207$ |
| $7$ | $146m$ | $K^x_7 = 0.544179$ $K^v_7 = 0.134328$ $\hat x_{7,7} = 147.23 \space m$ $\hat v_{7,7} = 19.97 \space m/s$ $p^x_{7,7} = 0.005442$ $p^v_{7,7}=0.005373$ |
$\hat x_{8,7} = 167.2 \space m$ $\hat v_{8,7} = 19.97 \space m/s$ $p^x_{8,7} = 0.01.815$ $p^v_{8,7} = 0.005373$ |
| $8$ | $165m$ | $K^x_8 = 0.519575$ $K^v_8 = 0.118421$ $\hat x_{8,8} = 166.06 \space m$ $\hat v_{8,8} = 19.71 \space m/s$ $p^x_{8,8} = 0.005196$ $p^v_{8,8}=0.004737$ |
$\hat x_{9,8} = 185.77 \space m$ $\hat v_{9,8} = 19.71 \space m/s$ $p^x_{9,8} = 0.009933$ $p^v_{9,8} = 0.004737$ |
| $9$ | $181m$ | $K^x_9 = 0.498309$ $K^v_9 = 0.105882$ $\hat x_{9,9} = 183.39\space m$ $\hat v_{9,9} = 19.21 \space m/s$ $p^x_{9,9} = 0.004983$ $p^v_{9,9}=0.004235$ |
$\hat x_{9,9} = 202.6 \space m$ $\hat v_{10,9} = 19.21 \space m/s$ $p^x_{10,9} = 0.009218$ $p^v_{10,9} = 0.004235$ |
| $10$ | $201m$ | $K^x_10 = 0.479665$ $K^v_10 = 0.095745$ $\hat x_{10,10} = 201.83\space m$ $\hat v_{10,10} = 19.05 \space m/s$ $p^x_{10,10} = 0.004797$ $p^v_{10,10}=0.00383$ |
$\hat x_{11,10} = 220.89 \space m$ $\hat v_{11,10} = 19.05 \space m/s$ $p^x_{11,10} = 0.008626$ $p^v_{11,10} = 0.004383$ |