向量(Vector)
对于向量这个概念,很多人都是既熟悉又陌生。可能是因为不同学科对向量的定义和表示存在一定的区别,造成大家的理解困难。
向量是什么
我们从数学,物理,计算机三个角度来看待如何定义⌈向量⌋。
物理专业角度
在物理学科中,一般将向量称为⌈矢量⌋,并且与⌈标量⌋一词相对。
向量是空间中的箭头。
决定一个向量的是:它的长度和它所指的方向。
计算机专业角度
向量是有序的数字列表。
向量不过是“列表”的花哨说法。
向量的维度等于列表的长度
数学专业角度
数学的本质就是通用和抽象,所以,数学家希望概况这两种观点:
向量可以是任何东西,只需要保证:两个向量相加以及数字与向量相乘是有意义的即可。
向量的加法和向量的乘法贯穿线性代数,十分重要。
如何表示向量
代数表示
在字母头上加一个箭头,来表示向量。例如:$\overrightarrow{v}$
几何表示
向量不需要从原点开始,它可以位于任何地方。换句话说,箭头是由它的长度和方向决定的,而不是由它的位置决定的。
下图所有的箭头都是表示向量 $\left( \begin{array}{c} 1 \\ 2 \end{array} \right)$, 图片来源
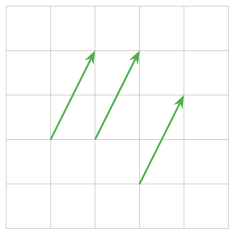
除非特殊说明,我们都假设所有向量都从原点开始。
坐标表示
把向量至于坐标系中,坐标正负表示方向,原点为起点,可把物理和计算机角度融合起来。
向量加法:
- 物理:收尾相连
- 计算机:坐标相加
向量乘法:
- 物理:缩放 Scaling
- 计算机:坐标和比例相乘
求一个向量的坐标表示:
已知两个点 $A \left( a, b \right)$ 和 $B \left( c, d \right) $,可以得到 $\overrightarrow{AB} = \left( \begin{array}{c} c-a \\ d-b \end{array}\right)$。